A 4DCT phantom
was created with MATLAB®, the phantom consists of 50 slices and 10
phases (512x512 slices with 1x1x2 mm3 voxel size).
The contour of
a synthetic 4D organ was designed within the phantom according to the following
2D polar equation
Rθ=a+b(sin(θ) - cisin(θ)cos(θ) + dicos(θ)) Eq.1
Where [6≤a≤8, -1≤b≤1.5, -3≤ci≤1,
1≤di≤2.5, i=slice number]
The contour was deformed through individual slices
and phases by applying different values to the a, b, c and d
coefficients of Eq.1, the values were chosen to achieve a smooth deformation
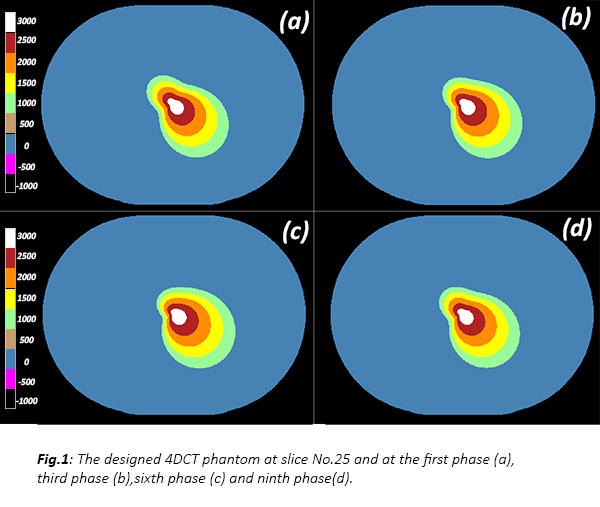
between consecutive phases and slices like human organs. The intensity values
within the contour were assigned to five discrete gradual values (1000 - 3000
HU) following the same polar equation and coefficients (see Fig.1).
Since coefficients (a) and (b)
are constants across phases, the radius Rθ of Eq.1 at any fixed
angle (θ) depends linearly on the coefficients (a,b,ci,di). Thus, the ground-truth Mid-P
contour in a slice is generated by using the mean coefficients of the 10
phases (a, b, mean(ci), mean(di))
in Eq.1. By repeating this to all slices we can create a time-weighted average
contour of the organ.
The intensity
values within the Mid-P contour were assigned similarly to the phantom. The
created phantom was used to test a Mid-P automated research prototype
(developed by Mirada Medical Ltd). The constructed Mid-P CT by the prototype
was compared to the ground-truth Mid-P CT using root mean-squared error (RMSE)
and the organ’s contour of the constructed Mid-P was compared to the
ground-truth contour using Dice similarity coefficient (DSC) and Hausdorff
distance.