Session Item

The accuracy of dose distributions in radiotherapy is limited by patient-related uncertainties (setup or anatomical changes), the interobserver variability (IOV) in target and OAR delineation and technical aspects (e.g. dose grid). Despite efforts to mitigate their impact (e.g. by means of IGRT), it is still necessary to account for them with PTV margins for treatment planning. An adequate margin reduction requires a comprehensive understanding of the relevant uncertainties and their effect on the final dose distribution.

Variance-based sensitivity analysis (SA) is a Monte-Carlo approach enabling the break-down of the total resulting uncertainty of a model into the contribution of the uncertain input parameters. A Matlab framework has been implemented for photon irradiations with which IMRT-plans for 10 meningioma patients were processed. The model included the simulation of patient setup shifts (standard deviation 0.5 mm), the IOV (12 target contours of 4 clinicians based on 3 different imaging modalities) and variating dose grids (1-3 mm). With these modeled uncertainties, ~10^4 independent dose calculations were performed with the open-source software MatRad. For optimization PTVs the delineated target contours were enlarged by 4.6 mm and for the evaluation a consensus contour by 1.6 mm (representing all influencing uncertainties not comprised in the simulation). The contribution of the input parameters to the resulting variance is expressed in sensitivity indices (SI): The first order SI describing the direct impact (S_1 = 1: only influential parameter) and total effect SI including interplay effects (S_T = 0: no influence at all).

DVH criteria were evaluated for the PTV, OAR structures and single voxel doses. Convergence of the results was achieved with the currently applied estimators for SI after ~3 days (512 runs corresponding to 7168 dose calculations). The DVH-distribution (fig. 1) was split up into the influence of the input parameters by means of SA (fig. 2). In 90% of the results the IOV (imaging or observer) is decisive for the target volume coverage (sum of both S_1 > 0.5).

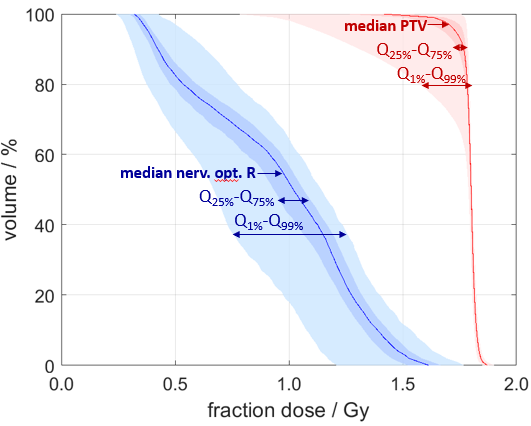
Fig. 1: Example for the variance in the resulting DVH for one OAR structure (blue) and the evaluation PTV (red) with corresponding percentiles.

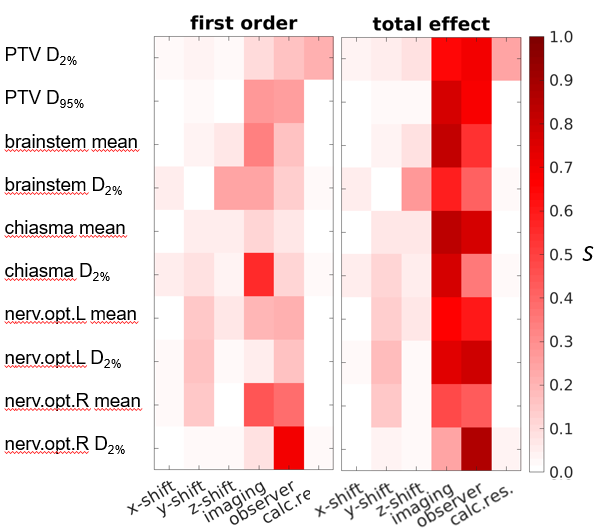
Fig. 2: First order (left) and total effect (right) SI of the input parameters patient setup shifts (shift_x/y/z), IOV (imaging and observer) and dose grid (calc.res.) for common DVH criteria for an exemplary patient.

Variance-based SA can be applied for the simultaneous and comprehensive investigation of the impact of several independent uncertain input parameters on the variance of dose distributions and plan quality criteria. First results for IMRT-plans in meningioma patients imply the applicability for comprehensive margin concept evaluation and the used framework can be adapted to address clinical questions and other entities.